ソウルカードの強化に必要な星屑の量とコスト感の目安について。
| 赤1 | 赤2 | 赤3 | 赤4, 赤5 | |||||
|---|---|---|---|---|---|---|---|---|
| 成功率 | 星屑 | 成功率 | 星屑 | 成功率 | 星屑 | 成功率 | 星屑 | |
| 0→1 | 100% | 250 | 100% | 500 | 100% | 800 | 100% | 1,200 |
| 1→2 | 100% | 280 | 100% | 560 | 100% | 900 | 100% | 1,350 |
| 2→3 | 100% | 310 | 100% | 610 | 100% | 1,000 | 100% | 1,490 |
| 3→4 | 100% | 340 | 100% | 680 | 100% | 1,090 | 100% | 1,640 |
| 4→5 | 100% | 370 | 100% | 740 | 100% | 1,180 | 100% | 1,770 |
| 5→6 | 100% | 400 | 100% | 800 | 100% | 1,280 | 100% | 1,920 |
| 6→7 | 85% | 620 | 85% | 1,240 | 85% | 1,980 | 85% | 2,970 |
| 7→8 | 80% | 800 | 80% | 1,600 | 80% | 2,560 | 80% | 3,840 |
| 8→9 | 75% | 1,140 | 75% | 2,280 | 75% | 3,650 | 75% | 5,480 |
| 9→10 | 70% | 1,310 | 70% | 2,620 | 70% | 4,200 | 70% | 6,290 |
| 10→11 | 65% | 1,550 | 65% | 3,100 | 65% | 4,960 | 65% | 7,440 |
| 11→12 | 60% | 1,780 | 60% | 3,560 | 60% | 5,700 | 60% | 8,550 |
| 12→13 | 55% | 2,460 | 55% | 4,920 | 55% | 7,880 | 55% | 11,820 |
| 13→14 | 50% | 3,080 | 50% | 6,160 | 50% | 9,860 | 50% | 14,790 |
| 14→15 | 50% | 3,350 | 50% | 6,160 | 50% | 9,860 | 50% | 14,790 |
| 15→16 | 50% | 6,160 | 50% | 9,860 | 50% | 14,790 | ||
| 16→17 | 50% | 6,160 | 50% | 9,860 | 50% | 14,790 | ||
| 17→18 | 50% | 6,160 | 50% | 9,860 | 50% | 14,790 | ||
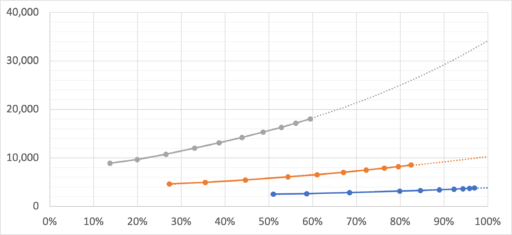
運良く成功すれば平均より少ない消費量で済み、不運が重なれば平均より多く消費することになる。詳細は後述するが、グラフは 12 回までの実線と、近似曲線から想定される平均消費量を示す。実際の成功確率が表示の確率と異なる可能性はここでは考慮しない。
赤1を例にすると、6→9 に 4000, 9→12 に 10000, 12→15 に 34000 ほどの星屑を消費するのが「普通」となる。
| 赤1 | 6→9 | 9→12 | 12→15 | 15→18 | ||||
|---|---|---|---|---|---|---|---|---|
| 確率 | 平均 | 確率 | 平均 | 確率 | 平均 | 確率 | 平均 | |
| 〜3回 | 51% | 2,560 | 27% | 4,640 | 14% | 8,890 | ||
| 〜4回 | 59% | 2,641 | 35% | 4,942 | 20% | 9,653 | ||
| 〜5回 | 68% | 2,830 | 45% | 5,453 | 27% | 10,772 | ||
| 〜6回 | 80% | 3,139 | 54% | 6,093 | 33% | 12,011 | ||
| 〜7回 | 85% | 3,274 | 61% | 6,560 | 39% | 13,122 | ||
| 〜8回 | 89% | 3,426 | 67% | 7,039 | 44% | 14,231 | ||
| 〜9回 | 92% | 3,569 | 72% | 7,496 | 49% | 15,311 | ||
| 〜10回 | 94% | 3,663 | 76% | 7,889 | 53% | 16,308 | ||
| 〜11回 | 96% | 3,744 | 80% | 8,227 | 56% | 17,162 | ||
| 〜12回 | 97% | 3,813 | 82% | 8,562 | 59% | 18,064 | ||
| 〜∞回 | 約4,000 | 約10,000 | 約34,000 | |||||
| 赤1 | 6→9 | 9→12 | 12→15 | 15→18 | ||||
|---|---|---|---|---|---|---|---|---|
| 確率 | 平均 | 確率 | 平均 | 確率 | 平均 | 確率 | 平均 | |
| 〜3回 | 51% | 5,120 | 27% | 9,280 | 14% | 17,240 | 13% | 18,480 |
| 〜4回 | 59% | 5,282 | 35% | 9,885 | 20% | 18,767 | 19% | 20,533 |
| 〜5回 | 68% | 5,660 | 45% | 10,906 | 27% | 21,003 | 25% | 23,100 |
| 〜6回 | 80% | 6,279 | 54% | 12,186 | 33% | 23,451 | 31% | 25,872 |
| 〜7回 | 85% | 6,547 | 61% | 13,121 | 39% | 25,653 | 37% | 28,441 |
| 〜8回 | 89% | 6,853 | 67% | 14,079 | 44% | 27,852 | 42% | 30,973 |
| 〜9回 | 92% | 7,138 | 72% | 14,991 | 49% | 29,988 | 46% | 33,440 |
| 〜10回 | 94% | 7,325 | 76% | 15,779 | 53% | 31,961 | 51% | 35,723 |
| 〜11回 | 96% | 7,488 | 80% | 16,454 | 56% | 33,650 | 54% | 37,697 |
| 〜12回 | 97% | 7,627 | 82% | 17,123 | 59% | 35,436 | 57% | 39,769 |
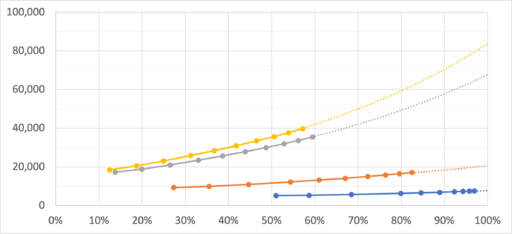
| 〜∞回 | 約8,000 | 約20,000 | 約68,000 | 約84,000 | ||||
| 赤1 | 6→9 | 9→12 | 12→15 | 15→18 | ||||
|---|---|---|---|---|---|---|---|---|
| 確率 | 平均 | 確率 | 平均 | 確率 | 平均 | 確率 | 平均 | |
| 〜3回 | 51% | 8,190 | 27% | 14,860 | 14% | 27,600 | 13% | 29,580 |
| 〜4回 | 59% | 8,448 | 35% | 15,829 | 20% | 30,046 | 19% | 32,867 |
| 〜5回 | 68% | 9,052 | 45% | 17,466 | 27% | 33,626 | 25% | 36,975 |
| 〜6回 | 80% | 10,043 | 54% | 19,515 | 33% | 37,546 | 31% | 41,412 |
| 〜7回 | 85% | 10,472 | 61% | 21,012 | 39% | 41,071 | 37% | 45,524 |
| 〜8回 | 89% | 10,960 | 67% | 22,547 | 44% | 44,592 | 42% | 49,576 |
| 〜9回 | 92% | 11,417 | 72% | 24,008 | 49% | 48,013 | 46% | 53,526 |
| 〜10回 | 94% | 11,716 | 76% | 25,270 | 53% | 51,172 | 51% | 57,180 |
| 〜11回 | 96% | 11,976 | 80% | 26,352 | 56% | 53,876 | 54% | 60,339 |
| 〜12回 | 97% | 12,198 | 82% | 27,423 | 59% | 56,736 | 57% | 63,656 |
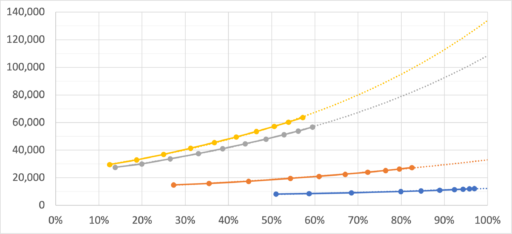
| 〜∞回 | 約12,000 | 約34,000 | 約108,000 | 約134,000 | ||||
| 赤1 | 6→9 | 9→12 | 12→15 | 15→18 | ||||
|---|---|---|---|---|---|---|---|---|
| 確率 | 平均 | 確率 | 平均 | 確率 | 平均 | 確率 | 平均 | |
| 〜3回 | 51% | 12,290 | 27% | 22,280 | 14% | 41,400 | 13% | 44,370 |
| 〜4回 | 59% | 12,677 | 35% | 23,732 | 20% | 45,068 | 19% | 49,300 |
| 〜5回 | 68% | 13,584 | 45% | 26,184 | 27% | 50,440 | 25% | 55,463 |
| 〜6回 | 80% | 15,069 | 54% | 29,257 | 33% | 56,319 | 31% | 62,118 |
| 〜7回 | 85% | 15,714 | 61% | 31,500 | 39% | 61,607 | 37% | 68,286 |
| 〜8回 | 89% | 16,446 | 67% | 33,800 | 44% | 66,888 | 42% | 74,365 |
| 〜9回 | 92% | 17,132 | 72% | 35,991 | 49% | 72,019 | 46% | 80,289 |
| 〜10回 | 94% | 17,580 | 76% | 37,882 | 53% | 76,758 | 51% | 85,771 |
| 〜11回 | 96% | 17,970 | 80% | 39,503 | 56% | 80,813 | 54% | 90,508 |
| 〜12回 | 97% | 18,303 | 82% | 41,109 | 59% | 85,104 | 57% | 95,485 |
| 〜∞回 | 約18,000 | 約51,000 | 約164,000 | 約201,000 | ||||
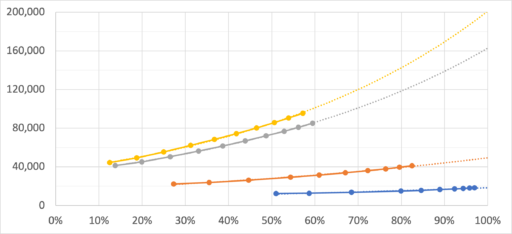
+6 から +9 までの強化を例に説明する。
6→7, 7→8, 8→9 のどの強化にに失敗しても +6 に戻るため、3回連続で成功しなくては +9 にならない。
3回の強化で済む確率は 0.85 × 0.80 × 0.75 = 0.51
この際の消費星屑は 620 + 800 + 1140 = 2560 となる。
4回の強化で済む成否のパターン数は1つ。失敗→成功→成功→成功 しかないので
4回の強化で済む確率は ( 1 – 0.85 ) × 0.85 × 0.80 × 0.75 = 0.0765
この際の消費星屑は 620 + 620 + 800 + 1140 = 3180 となる。
4回までで済む確率は 0.51 + 0.0765 = 0.5865
この「4回までで済むケースの中」での確率的な平均消費量は
( 0.51 × 2560 + 0.0765 × 3180 ) ÷ 0.5865 = 2641 となる。
あとは成否のパターンを網羅しながら考慮する回数を増やしていく。
\( \displaystyle \lim_{n \to \infty} \) で収束しそうなら、そこが最終的な平均消費量と想定できる。
表の星屑の単位は千個。+15 以降は精錬の +15% を考慮済み。
表の左上が割安、右下が割高。
| 強化 | +12 | +15 | +18 | +18 | +15 | +18 | |
|---|---|---|---|---|---|---|---|
| 平均消費星屑 | 78 | 240 | 441 | 441 | 240 | 441 | |
| 個数 | 1個 | 2個 | 3個 | 2個 | 1個 | 1個 | |
| 虹5 | 2.40% | 33 | 43 | 53 | 80 | 87 | 160 |
| 赤5 | 2.00% | 39 | 52 | 64 | 96 | 104 | 192 |
| 虹4 | 1.80% | 43 | 58 | 71 | 107 | 116 | 213 |
| 赤4 | 1.50% | 52 | 70 | 85 | 128 | 139 | 256 |
| 虹5(刻印) | 1.20% | 65 | 87 | 107 | 160 | 174 | 320 |
| 赤5(刻印) | 1.00% | 78 | 104 | 128 | 192 | 209 | 383 |
| 虹4(刻印) | 0.90% | 87 | 116 | 142 | 213 | 232 | 426 |
| 赤4(刻印) | 0.75% | 104 | 139 | 170 | 256 | 278 | 511 |
ゲーム画面に表示される精錬の +15% の効果は、百分率の小数点二桁まで正しいケースと 0.01% 不足しているケースがある。表示上の問題か、実際の効果が表記通りなのか、詳しくは不明。浮動小数点の誤差や切り捨てと絡んでいそうな予感。
例えば 単精度浮動小数点 を用いると
+2.00% つまり 0.02 は 0.019999999552965164
+2.40% つまり 0.024 は 0.024000000208616257
それを 倍精度浮動小数点 に変換 (キャスト) して 1.15 を掛けると
+2.00% × 1.15 = 0.022999994859… で切り捨てて +2.29% となり
+2.40% × 1.15 = 0.027600000239… で切り捨てて +2.76% となる。
最終的な合計値は、個々に切り捨てられた値の合計のように見える。
Protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
まだコメントがありません。